Matriks adalah susunan bilangan yang di tulis dalam bentuk persegi panjang dan di susun dalam baris serta kolom. Setiap angka dalam matriks di sebut elemen. Kamu akan sering menemukan matriks ditulis menggunakan tanda kurung biasa ( ) atau kurung siku [ ]. Dalam dunia matematika, matriks menjadi alat penting untuk menyelesaikan banyak persoalan, mulai dari hitungan sederhana hingga perhitungan kompleks dalam teknologi.
Misalnya, jika kamu punya data nilai siswa dalam kelas, kamu bisa menuliskannya dalam bentuk matriks agar lebih rapi dan mudah di baca. Matriks membantu kita mengatur data dengan terstruktur sehingga proses perhitungan menjadi lebih cepat dan efisien. Tidak heran, materi matriks sering di ajarkan di sekolah menengah hingga perguruan tinggi karena sangat berguna dalam berbagai bidang ilmu.
Jenis-jenis Matriks dan Contohnya
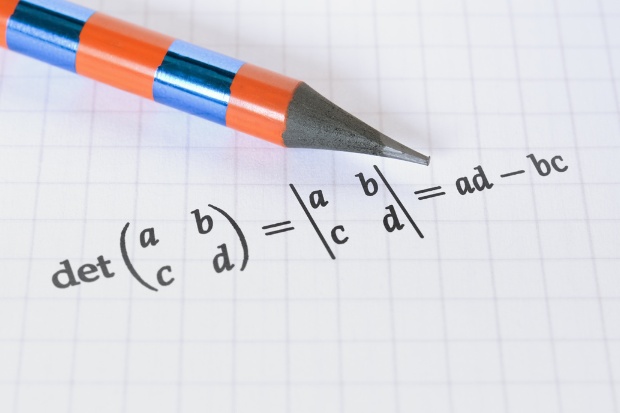
Matriks memiliki berbagai jenis, dan setiap jenis punya ciri khas serta kegunaan masing-masing. Berikut beberapa di antaranya:
- Matriks Baris – Matriks yang hanya memiliki satu baris, contohnya:
[2 5 7] - Matriks Kolom – Matriks yang hanya memiliki satu kolom, contohnya:
[3] [6] [9] - Matriks Persegi – Matriks dengan jumlah baris dan kolom yang sama, contohnya matriks 2×2:
[1 2] [3 4] - Matriks Nol – Matriks yang semua elemennya bernilai nol.
- Matriks Identitas – Matriks persegi dengan elemen diagonal bernilai 1 dan elemen lainnya bernilai 0.
Setiap jenis matriks ini punya peran penting. Misalnya, matriks identitas sering di gunakan dalam perhitungan balik (inverse) matriks, sedangkan matriks nol di gunakan sebagai penanda awal data sebelum di isi nilai sebenarnya.
Operasi Dasar pada Matriks
Saat belajar matriks, kamu akan menemukan berbagai operasi dasar. Beberapa di antaranya adalah:
- Penjumlahan Matriks – Kamu bisa menjumlahkan dua matriks jika ukurannya sama. Caranya, tambahkan elemen yang posisinya sama pada kedua matriks.
- Pengurangan Matriks – Hampir sama seperti penjumlahan, hanya saja kamu mengurangkan elemen yang posisinya sama.
- Perkalian Matriks dengan Skalar – Setiap elemen matriks di kalikan dengan suatu bilangan.
- Perkalian Matriks – Lebih kompleks, karena setiap elemen pada baris matriks pertama di kalikan dengan elemen pada kolom matriks kedua, lalu di jumlahkan hasilnya.
Operasi-operasi ini adalah dasar penting untuk mempelajari langkah lebih lanjut seperti mencari determinan atau inverse matriks.
Penerapan Matriks dalam Kehidupan Sehari-hari
Matriks bukan hanya ada di buku pelajaran. Banyak teknologi di sekitar kita yang bekerja menggunakan prinsip matriks. Contohnya:
- Pengolahan Gambar Digital – Foto yang kamu lihat di ponsel adalah kumpulan piksel yang di susun seperti matriks.
- Sistem Navigasi GPS – Matriks membantu menghitung posisi dan rute tercepat.
- Ilmu Ekonomi – Matriks di gunakan untuk menganalisis data produksi, penjualan, dan distribusi.
- Desain Grafis dan Animasi – Efek rotasi, perbesaran, atau pengecilan gambar bisa di hitung dengan matriks.
Kalau kamu membaca artikel tentang pendidikan di Sobat Kabar, kamu akan menemukan banyak contoh seru lainnya yang membuat konsep matematika terasa lebih dekat dengan kehidupan kita.
Cara Menghitung Determinan Matriks
Determinannya seperti “nilai khusus” dari matriks, terutama matriks persegi. Untuk matriks 2×2, cara menghitungnya sangat mudah. Misalnya matriks:
[a b]
[c d]
Determinannya di hitung dengan rumus:Det = (a × d) – (b × c)
Jika kamu punya matriks 3×3, langkahnya sedikit lebih panjang. Kamu bisa menggunakan metode Sarrus atau ekspansi kofaktor. Prinsipnya tetap sama, yaitu mengalikan elemen pada diagonal tertentu lalu menguranginya dengan hasil perkalian diagonal lainnya. Menguasai cara menghitung determinan akan sangat membantu jika kamu ingin mempelajari aljabar linear lebih dalam. Baca juga artikel lainnya di hangatin mulai dari kategori bisnis, inspiratif, dan lain-lain.
Kesimpulan
Matriks adalah salah satu konsep penting dalam matematika yang memiliki manfaat luas, mulai dari pengaturan data, perhitungan ilmiah, hingga penerapan teknologi canggih. Kita telah membahas pengertian, jenis-jenis, operasi dasar, penerapan dalam kehidupan sehari-hari, dan cara menghitung determinan. Dengan memahaminya, kamu akan lebih mudah mengikuti pelajaran matematika dan mengaplikasikannya dalam kehidupan nyata. Jadi, jangan takut dengan matriks. Anggap saja ini adalah alat yang mempermudah perhitungan dan membuat data lebih rapi.

